The Consumer Price Index:
A Way to Compare Prices in Different Years
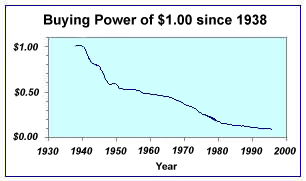
Inflation is a decline in the value of money in relation to the goods that it can buy and is a pervasive economic phenomenon. It is so pervasive that it is very difficult to compare this year’s prices to last year’s, much less compare prices over decades. Here is a graph of the buying power of $1.00 since 1938:

How is the "buying power" of $1.00 measured? How can we compare prices of item in different years? The answer is the use of price indices such as the consumer price index or CPI. Below is a simplified explanation of how the indices are created and how we can use them. Economists choose a base year and determine the price of a "bundle" of goods: food, clothing, housing costs, transportation costs, services, entertainment in varying proportions. The proportions for the index we are using (CPI(U)) are
Components of the CPI(U) |
|
| Housing | 41.4% |
| Transportation | 17.8% |
| Food | 16.2% |
| Energy | 8.2% |
| Medical Care | 6.4% |
| Apparel and Upkeep | 6.1% |
| Other | 3.9% |
The cost of this bundle in one year is assigned an index number. The next year, the cost of the same bundle is determined. The CPI for that year represents the new cost of the bundle.
The Table below shows the official CPI since 1982. We will explore how it is used.
Year |
CPI |
1982 |
96.5 |
1983 |
99.6 |
1984 |
103.9 |
1985 |
107.6 |
1986 |
109.6 |
1987 |
113.6 |
1988 |
118.3 |
1989 |
124.0 |
1990 |
130.7 |
1991 |
136.2 |
1992 |
140.3 |
1993 |
144.5 |
1994 |
148.2 |
1995 |
152.4 |
1996 |
156.9 |
1997 |
160.5 |
1998 |
163.0 |
The beauty of this table is that we can easily compare any two years prices. For example, from the table we can see that
in 1982, it would cost $96.50 for goods and services costing $113.60 in 1987.
But also from the table we can see that
in 1994, it would cost $148.20 for goods and services costing $113.60 in 1987.
We can therefore say that $96.50 in 1982 is equivalent to $113.60 in 1987 which is equivalent to $148.20 in 1994.
This information will allow us to calculate how many times more the prices of goods were in one year than in another. Using 1982 and 1994 as an example, we can calculate the ratio of the CPI values for those two years:
![]()
The CPI allows you to convert anything money related (prices, wages, salaries) from one year to another. For example, let's say your father said he made $7,000 a year at one of his first jobs in 1965. That doesn't sound like a lot of money to us today, but we must consider that everything was less expensive in 1965. What is that salary worth in today's money? To answer that, we can convert the $7000 to 2005 constant dollars using the CPI values for those years.
The CPI table tells us that
31.5 in 1965 dollars is equivalent to 195.3 in 2005 dollars.
We wish to know
$7000 in 1965 dollars is equivalent to ? in 2005 dollars.
One way to conceptualize the conversion to constant dollars is to focus on the meaning of the ratio of the CPI's (found in CPI.xls):
![]()
This ratio tells us that one dollar in 1965 is equivalent to $6.20 in 2005. Another way to think about it is that prices were, on average, 6.2 times more in 2005 than in 1965. Multiplying the wage of $4000 by this ratio completes the conversion
7000 * 6.2 = 43,400
This means that your father's $7000 salary is equivalent to making $43,400 a year today.
This interpretation of the CPI also allows us to compare prices in two different years and determine when an item was more expensive. We can calculate whether an item increased in price at the same rate as the "bundle of goods" or at a faster or slower rate.
For example, the price of gasoline in 1990 was $1.16 per gallon on average. In 2004, it averaged $1.85. Was gasoline more expensive or less expensive in 2004?
On the face of it, it seems that gas is more expensive in 2004. The actual price is definitely higher in 2004, but that is to be expected. The prices of (almost) everything are higher in 2004 than in 1990. But just comparing the actual prices does not take the changing value of money into consideration. To compare the prices taking into account inflation, we convert one of the prices to the same year as the other. Usually, we convert forward to the more recent year. In our example, we want to convert $1.16 1990 dollars to its equivalent in 2004 dollars. Using the CPI values (found in CPI.xls):
2004 CPI/1990 CPI *1990 price = 1990 price in constant 2004 dollars
188.9 / 130.7 * 1.16 = $1.68
What this tells us is that $1.16 in 1990 was equivalent to $1.68 in 2004. $1.68 is the 1990 price in constant 2004 dollars. In other words, when Americans paid $1.16 per gallon for gasoline in 1990, it was equivalent to paying $1.68 in 2004. We can now compare the actual price in 2004 to the 1990 price in constant 2004 dollars. Since $1.68 is less than the $1.85 that people were actually paying in 2004, gasoline was less expensive in 1990 than it was in 2004.
Try a similar calculation comparing the price of gas in 1990 to the price of gas in 2000 which was $1.51. Again, nominally, the price in 2000 is larger than the price in 1990, but that is to be expected. When did it "feel" more expensive to buy gas? convert the 1990 price to its 2000 constant dollar equivalent by multiplying the 1990 price by the ratio of the CPI values in 2000 and 1990:
![]()
![]()
The general formula for converting to constant dollars :
"new" CPI / "old" CPI * old price = Price in constant dollars
__________________________________________________________________________________________________________
Another use of the CPI is to convert an entire series of prices to constant dollars. For example, consider the price of electricity from 1986 to 1997:
|
Electricity Prices (US city average, per KWH) |
|
|
|
|
|
Year |
Price |
|
1986 |
$0.077 |
|
1987 |
$0.079 |
|
1988 |
$0.080 |
|
1989 |
$0.082 |
|
1990 |
$0.084 |
|
1991 |
$0.087 |
|
1992 |
$0.088 |
|
1993 |
$0.092 |
|
1994 |
$0.092 |
|
1995 |
$0.094 |
|
1996 |
$0.094 |
|
1997 |
$0.094 |
In graphical form, the data looks like:

The graphs shows the price of electricity rising from a minimum of 7.7¢ per kilowatt-hour in 1986 to its maximum in 1997 of 9.4¢. Since the value of the dollar decreased each year, this graph is not a realistic depiction of electricity costs over this period. While this graph does show that the nominal cost of electricity rose each year, it is incorrect to assume that electricity became more expensive over the years. To get a more accurate understanding, we should convert the entire data series to constant 1997 dollars. The spreadsheet below depicts the calculation. First one would copy and paste the CPI values from CPI.xls. Next one would fill a column with the "old" actual price multiplied by the ratio of the CPI's involved.
| Electricity Prices (US city average, per KWH) | |||
| 1986 | $0.077 | 109.6 | =$C$13/C2*B2 |
| 1987 | $0.079 | 113.6 | $ 0.112 |
| 1988 | $0.080 | 118.3 | $ 0.109 |
| 1989 | $0.082 | 124.0 | $ 0.106 |
| 1990 | $0.084 | 130.7 | $ 0.103 |
| 1991 | $0.087 | 136.2 | $ 0.102 |
| 1992 | $0.088 | 140.3 | $ 0.101 |
| 1993 | $0.092 | 144.5 | $ 0.102 |
| 1994 | $0.092 | 148.2 | $ 0.100 |
| 1995 | $0.094 | 152.4 | $ 0.099 |
| 1996 | $0.094 | 156.9 | $ 0.096 |
| 1997 | $0.094 | 160.5 | $ 0.094 |
You might wonder why you don't use the formula =C13/C2*B2. This formula will not fill correctly, since C13 needs to be used again in each cell (not C14, C15, ...). You need to either enter the "new" CPI as the actual number. Another correct formula for this cell is =$C$10/C2*B2 which uses an absolute cell reference for C13. To get an absolute cell reference, enter the cell reference then hit the F4 button on the top of the keypad. (You could also manually enter the dollar signs before and after the letter OR you can just enter the number in that cell instead of a cell reference). An absolute cell reference tells Excel to keep that cell the same in the subsequent calculations.
Here is the graph of electricity costs in constant 1997 dollars:
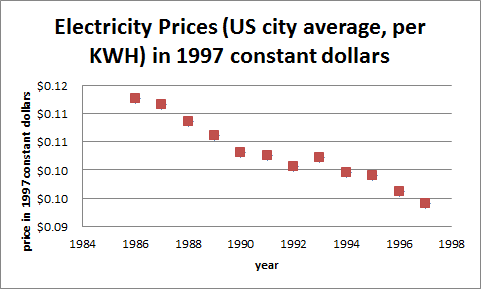
In fact, electricity costs went down every year except one from 1990 to 1997. In constant 1997 dollars, electricity costs were at their highest in 1986, when they were nearly 11.2¢ per kilowatt-hour. The cost dropped every year except 1993. The minimum was in 1997, at 9.4¢ per kilowatt-hour. The graph in constant dollars tells a very different (and more realistic) story of electricity costs. It shows that the cost of electricity, when inflation has been taken into account, has decreased over the years meaning it has become less expensive.
Graphs of prices in constant dollars tell you whether the price of an item has grown faster, slower, or at the same rate as inflation. If the graph increases, it has grown faster than inflation, it has become more expensive; if it decreases, it has grown slower, it has become less expensive; and if it is a flat horizontal line, it has grown at the same rate as inflation.
Finally, the inflation rate is defined as the percentage change in the CPIs from the previous year to the next. For example, the inflation rate in 1996 was
![]()