Solutions to Assignment 4
The problems you should study for the
final exam are marked with a (***).
***1. Classify each of the following statements as an example of theoretical
probability, relative frequency interpretation of probability, or personal
(subjective) probability.
a. According to company records the probability that a washing machine will
need repairs during a six year period is 0.10.
Because of the phrase "according to company records," the
sentence suggests that the probability figure was based on the relative
frequency of repairs.
b. The probability of choosing six number from 1 to 40 that match the six
numbers drawn by a state lottery is 1/3,838,380 » 0.00000026.
All 3,838,380 possibilities are viewed as equally
likely on theoretical grounds.
c. If Rex Grossman plays well, the Bears have a 75% chance of making it to
the Super Bowl.
This statement is an example of subjective probability,
a person's assessment of likelihood, not based on any repeated trials. In
fact, the situation in question is not repeatable. In a different year, it
would be a different Bears team against different opponent teams, etc.
d. We think there is a 50-50 chance of a recession next year.
This statement is another example of subjective
probability.
e. The probability of a person from the United States being left handed is
0.11.
This statement suggests that it was based on a census
or survey of some kind; hence, most likely it is an example of probability as a
relative frequency.
***2. The following data from the US Census Bureau (http://www.census.gov/prod/2002pubs/p20-542.pdf)
indicates the age distribution of voters in the 2000 presidential election:
| Ages of voters |
Frequency (millions) |
| 18 to 24 years old |
32.3 |
| 25 to 44 years old |
49.8 |
| 45 to 64 years old |
64.1 |
| 65 years and over |
67.6 |
a. What is the probability that a voter chosen randomly from
these voters is 18 to 24 years old?
32.3/(32.3+49.8+64.1+67.6)
≈ 0.151
b. What is the probability that a voter chosen randomly from
these voters is over 45 years old?
(64.1+67.6)/(32.3+49.8+64.1+67.6)
≈ 0.616
c. Suppose you choose two random voters. What is
the probability that both are 18 to 24 years old?
Choosing two random voters can be
viewed as essentially independent events, since the number of voters is so
large. (In general, choosing without replacement is not independent.)
So the probability is
0.151*0.151 ≈ 0.0228
***3. Suppose a family has four children.
a. Describe the sample space for the gender distribution
(boy, girl, boy, boy etc) of the four children. Note: the order
matters! There are sixteen possibilities.
BBBB, BBBG, BBGB, BBGG, BGBB, BGBG, BGGB, BGGG, GBBB,
GBBG, GBGB, GBGG, GGBB, GGBG, GGGB, GGGG
b. If the probability of having a male baby is 0.512, what
is the probability of having four girls?
The probability of having one girl is
1 – 0.512 = 0.488. The probability of
four girls is 0.488^4 ≈ 0.0567. This event is fairly uncommon.
(skip) c. Simulate this scenario in Excel as follows. In
Column H type:
Then generate 10000 rows of four 0's and 1's based on
the theoretical probability.
0
Paste the top 10 rows of your simulation into your Word
document.
Here is what I got. The fifth column
as is the sum of the four columns.
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
3 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
3 |
|
1 |
0 |
1 |
1 |
3 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
4 |
|
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
(skip) d. Using your simulation, calculate the relative frequency
of having all girls. You should get an answer fairly close to the answer you
got in part b. (Hint. The way I would do this is to add up each row
and then count how many rows add up to 4, but there are other ways as well.)
I got 564/10000 = 0.0564 which is quite close to the
theoretical 0.0567.
(skip) e. What is more likely in a family of four: having two
boys and two girls or having three of one gender and one of the
other gender? Your answer should include the calculation of the
probability for each scenario. Hint. You can do this
theoretically or you can use your simulation to obtain a very close
approximation to the theoretical probability. If you proceed theoretically, use the sample space to
count how many possibilities there are in each case. You have to
consider two subcases in calculating the probability of having three of one
gender and one of the other gender, namely the case of three girls and one
boy and the case of three boys and one girl. If you use your
simulation, use COUNTIF.
The theoretical probability of having
two boys and two girls is 6*(0.512)^2*(0.488)^2 ≈ 0.375 (there are 6 ways:
BBGG, BGBG, BGGB, GBBG, GBGB, GGBB). The theoretical probability of having three of one
and one of the other is 4*(0.512)^3*0.488 + 4*0.512*(0.488)^3 ≈
0.5.
(skip) f. Did the result of part e surprise you? Why or why not?
This result surprised me the first time I heard it.
If you make a graph of the probabilities, one gets an idea of what is going
on. The two bars next to the middle bar add up to more than the middle
bar. Intuitively, it seems that the two bars next to the middle one should
be smaller than they really are.
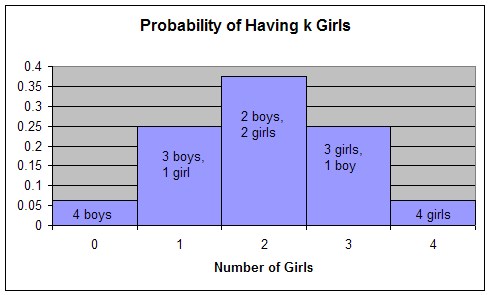
***4. The distribution of ABO and Rh blood type
for both men and women in the US is given in the table below:
| |
|
ABO blood type |
|
| |
|
O |
A |
B |
AB |
Total |
|
Rh Factor |
Rh
positive |
38.4% |
32.3% |
9.4% |
3.2% |
|
|
Rh negative |
7.7% |
6.5% |
1.7% |
0.7% |
|
| | Total | | | | |
|
The first thing I would do is
calculate the marginal probabilities:
|
|
|
ABO blood type |
|
|
|
|
O |
A |
B |
AB |
Total |
|
Rh Factor |
Rh positive |
38.4% |
32.3% |
9.4% |
3.2% |
83.3% |
|
Rh negative |
7.7% |
6.5% |
1.7% |
0.7% |
16.6% |
|
|
Total |
46.1% |
38.8% |
11.1% |
3.9% |
99.9% |
Note that because of rounding, the
total is 99.9% rather than 100%.
a. What is the probability that a randomly selected
person is B negative?
1.7%
b. What is the probability that a randomly selected person
in the US is Rh negative?
16.6%.
c. An individual with type B blood can safely receive
transfusions only from persons with type B or type O blood. What is the
probability that the husband of a woman with type B blood is an acceptable blood
donor for her?
46.1% + 11.1% = 57.2%
d. What is the probability that in a randomly chosen
couple, the wife has type B blood and the husband has type A?
0.111*0.388 = 0.043
e. What is the probability that in a randomly chosen
couple, one of the pair has type A blood and the other has type B?
2*0.111*0.388 = 0.086
(skip) f. What is the probability that at least one of a
randomly chosen couple has type O blood?
The easiest way to calculate this is
to calculate the probability of the complementary event. The complementary
event is both not having O blood. The probability of not having O blood is
1 – 0.461 = 0.539. The probability of both
not having O blood is 0.539*0.539. So the probability of at least one
person having O blood is 1 –0.539*0.539 = 0.709. It is rather high
likelihood.
(skip) g. There are medical risks for subsequent pregnancies if a
mother and her child have different Rh factors. What is the probability
that a randomly chosen couple have different Rh factors? (Hint. Remember
that the male can be positive and the female negative and vice versa.)
(Biology note: It is possible for a child and mother to have different Rh
factors even if they both parents have the same Rh factor if the parents are
carriers of the negative Rh factor gene.)
The husband can be + and the wife can
be – and vice versa. So the probability is
2*(0.833)*(0.166) ≈ 0.277.
(skip) 5. When tossing a coin, a "run" is a string of
consecutive results that are all the same. For example, in the sequence T
T H H T T T T H T there is a run of length 2 (two T's)
followed by a run of length 2 (two H's), followed by a run of length 4 (four
T's), followed by a run of length 1 (one H), and final run of length 1 (one T).
The longest run in this case is one of length 4. Open the file
SequencesOfTenCoinFlips.xls.
This file contains the results of 50,000 sequences of 10 coin flips. As usual,
"1" denotes heads, and "0" denotes tails. In addition, all but the top ten
rows of Column L are filled with the length of the longest run for the coin flip
sequence in that row.
a. Fill in the top 10 rows and paste the top 10 rows of
Column L into your Word document. (Hint. I'll get you started. In row 1,
the run lengths are 3, 1, 3, and 3, so the first number is 3.)
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
3 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
3 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
3 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
4 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
2 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
3 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
5 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
4 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
2 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
|
3 |
b. Fill in the following table based on the simulation data
and paste it into your Word document.
|
Length of longest streak |
Frequency |
Percentage |
|
1 |
92 |
0.2% |
|
2 |
8397 |
16.8% |
|
3 |
18155 |
36.3% |
|
4 |
12454 |
24.9% |
|
5 |
6193 |
12.4% |
|
6 |
2745 |
5.5% |
|
7 |
1161 |
2.3% |
|
8 |
478 |
1.0% |
|
9 |
225 |
0.5% |
|
10 |
100 |
0.2% |
Hint. The answer for example for 6 is: 6 was the
longest streak in 2745 of the 50000 cases. So the frequency is 2745, and the
percentage is 2745/50000 or about 0.0549.
c. Based on the data in the table you created in part
b, what is the
probability that there will be a streak of 5 or more in a sequence of 10 coin
tosses?
12.4% + 5.5% + 2.3% + 1.0% + 0.5% +
0.2% = 21.8%
d. Do you find the result in part c surprising? Why or why
not?
The first time I came across this
result, I was surprised. Long streaks happen rather frequently! One
really shouldn't be too surprised to encounter a streak of 5 or more.
***7. What is the probability of getting a sum of 8 on a
roll of two dice?
The sample space can be visualized
as:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
(1,5) |
(1,6) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
(2,5) |
(2,6) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
(3,5) |
(3,6) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
(4,5) |
(4,6) |
|
5 |
(5,1) |
(5,2) |
(5,3) |
(5,4) |
(5,5) |
(5,6) |
|
6 |
(6,1) |
(6,2) |
(6,3) |
(6,4) |
(6,5) |
(6,6) |
The cells shaded in yellow show how
many ways one can get a sum of 8. The probability is 5/36 or about
0.139.
*** 8. A common data collection method in consumer and market research is the
telephone survey. However, a major problem with consumer telephone surveys
is nonresponse. A nonresponse can result from a person not being home, a
person not answering, a person refusing to participate, etc. Research has shown
that the probability of a successful response to a telephone survey is 0.08.
a. What is the probability of a nonresponse on a random
survey telephone call?
1 – 0.08 = 0.92.
b. What is the probability of having at least one
successful response out of three calls?
Once again, it easier to calculate
the probability of the complementary event. The complementary event is the all
three calls will be unsuccessful. The probability that all three will be
unsuccessful is 0.92^3 ≈ 0.779. So the
probability that at least one will be successful is 1 – 0.779 = 0.221.
c. What is the probability that in a sequence of
random telephone calls for a survey, that the first successful response will be
on the fifth one?
0.92*0.92*0.92*0.92*0.08
≈ 0.0573
(skip) d. (Extra credit) What is the probability that it
will take at least five phone calls before you have the first successful survey?
An elementary way calculating this
probability is to make a table:
|
|
Probability |
|
|
First success on first |
0.08 |
0.0800 |
|
First success on second |
0.92*0.08 |
0.0736 |
|
First success on third |
0.92*0.92*0.08 |
0.0677 |
|
First success on fourth |
0.92*0.92*0.92*0.08 |
0.0623 |
|
First success on fifth |
0.92*0.92*0.92*0.92*0.08 |
0.0573 |
|
etc |
etc |
|
We want to calculate the part of the
table that is shaded yellow, which is actually an infinite list. Adding up
the infinite list is possible, but it is easier to realize that the entire table
has to add up to 1, so the probability we are interested in is 1 – (0.080 + 0.0736 + 0.0677 + 0.0623) ≈ 0.716.
So it would be extremely common to have to make at least 5 calls.
